

This section makes no attempt to address the topic of Lagrangian Relaxation in great detail. Instead, this section is intended to give the user an overview of what Lagrangian Relaxation is and how it was implemented to solve the P-Median Problem.
Mathematically, the P-Median problem can be summarized as follows:
InputsThe objective function, (a), minimizes the total demand-weighted distance between each "customer" and the nearest facility. The constraints insure that the various properties of the problem are enforced. Specifically:

Decision Variables

Minimize
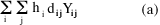
Subject to

Because of the binary constraints (e) and (f), the formulation above cannot be solved with standard linear programming techniques. This is where Lagrangian Relaxation comes in. Lagrangian relaxation is based on the premise that removing constraints from a problem makes the problem easier to solve. Therefore, to solve a problem, Lagrangian relaxations remove a constraint but introduces a penalty for violating the removed constraint. This revised problem is then optimized accordingly. The following is a decomposition of how the technique of Lagrangian relaxation was implemented to solve the P-Median problem:
Step 1: Setting up:We remove constraint (b) and add the constraint and a vector of variables called Lagrange multipliers to the objective function. For this particular implementation, the Lagrange multipliers were all initialized to a value of 300. The following problem is then obtained:
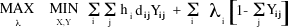
Step 2: Solving the simplified problem
For fixed values of the Lagrange multipliers, the objective function in the previous step is minimized by computing the value of setting each of the location variables(X) to 1. This value is given by:
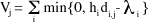
for each candidate location j. The P smallest values of V is then determined and the corresponding location variables (X) are set to 1 and all other location variables (X) to 0. The allocation variables (Y) are then set to:
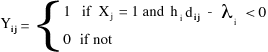
Step 3: Updating the lower bound and upper bound
For each iteration of this process, an upper bound of the objective function (estimate of a worst case scenario) and a lower bound (an optimistic estimate of the best case scenario) need to be determined. An upper bound is a solution that has been discovered which meets the constraints of the original unmodified problem. The lowest upper bound (best guess for the worst case) is sought for the purposes of this algorithm. The upperbound can be determined by simply determining the location closest to each customer. The corresponding allocation variables(Y) are then set to 1 while all others are set to 0. We then evaluate the P-Median objective function as stated originally.
Note that a solution to the simplified problem as outlined in Step 2, may or may not meet the constraints of the original problem. Since the modified problem need not meet the constraints of the original, the modified problem will produce an answer which will always be better or equal to the solution of the original problem. Thus, a lower bound on the P-Median problem can be determined by simply evaluating the original P-Median objective function using the values for the variables determined in Step 2 .
Step 4: Modifying the Lagrange multipliers
A technique that drives the iterations to an optimal solution that meets the constraints of the original problem called subgradient optimization is used to update the value of the Lagrange Multipliers; the details of which are beyond the scope of this section. Based on subgradient optimization, a new variable t is introduced and defined as follows:

The Lagrange multipliers are then updated according the following equation:
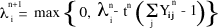
Step 5: Evaluating the results
If at any point in time, the lower bound is equal or very close to the upper bound, then chances are, the optimal solution to the original problem has been found and the algorithm in this case terminates. To put a reasonable cap on the run time of the algorithm, this applet limits the number of iterations to 100 and values of A to be no less than 0.01. If the upperbound has not decreased after 4 consective iterations, A is set to be A / 2. If none of the above stopping conditions are met, the implementation reiterates starting at Step 2.